INSTITUTO TECNOLÓGICO DE ACAPULCO
INGENIERÍA DE CONTROL CLÁSICO
UNIDAD 5
INTEGRANTES DEL EQUIPO:
*JOSE EDUARDO GARCÍA FLORES "JEFE DE EQUIPO" "10320564"
*ÁNGEL SALVADOR GALEANA ARCOS
*GUSTAVO NAVA CASTRO
Unidad 5
Estabilidad
5.1 Criterio de Routh-hurwitz
El teorema de Routh–Hürwitz sirve para analizar la estabilidad de los sistemas dinámicos.
Básicamente, el teorema proporciona un criterio capaz de determinar en cuál semiplano (izquierdo o derecho) del plano complejo están localizadas las raíces del denominador de la función de transferencia de un sistema; y en consecuencia, conocer si dicho sistema es estable o no. Si tras aplicar el criterio nos da como resultado que todos los polos están en el semiplano izquierdo, el sistema es estable, y si hay un mínimo de un polo en el semiplano derecho, el sistema es inestable.
El criterio se refiere a la función de transferencia en lazo cerrado del sistema. Para aplicar el criterio a un sistema descrito por su función de transferencia en lazo abierto, hay que incluir la realimentación haciendo: 1
El criterio de Routh-Hurwitz también se utiliza para el trazado del lugar de las raíces. En este caso, dicho procedimiento de análisis estudia la función de transferencia del sistema en bucle abierto 1+K·Gba(s)=0 (siendo K la ganancia variable del sistema). Su objetivo es determinar los puntos de corte del LdR con el eje imaginario. Dichos puntos marcan el límite de estabilidad del sistema, dicho en otras palabras, determinan el límite en el que los polos del sistema en bucle cerrado pasan al semiplano derecho complejo y por lo tanto el sistema se vuelve inestable. Como es evidente, tras la aplicación del criterio de Routh-Hurwitz, los resultados obtenidos quedarán en función de la ganancia K, lo cual nos indicará a partir de qué valores de K el sistema pasará de estable a inestable (ganancia K límite).
Procedimiento
Dado el sistema:
donde G (s) es la ecuación característica de un sistema.
El número de cambios de signo de: an, an-1, α1, β1, …, γ1, δ1 (primera columna resultante del criterio de Routh – Hürwitz), nos da la cantidad de elementos que están en el semiplano derecho. Si todos los elementos tienen el mismo signo, el sistema será asintóticamente estable, en cambio, si encontramos cambios de signo, el sistema será asintóticamente inestable. Como está indicado arriba, tendremos tantos polos en el semiplano positivo como variaciones de signo en la primera columna.
Ejemplo
Ejemplo: G(s) = 

Esto nos da como resultado en la primera columna: 1, 5, 2´8, -2´57, 2, con lo que por haber dos cambios de signo, el sistema es inestable por poseer dos elementos (-2,57 y 2) con cambio de signo.
Degeneraciones
Hay dos casos de degeneraciones:
- En la primera, el primer elemento de una fila de la tabla es 0. Esta degeneración se salva sustituyendo el 0 por “ε” (número infinitesimalmente positivo), y se continua calculando. Luego a la hora de comprobar los cambios de signo se deja el 0 que sustituimos y donde nos aparezca “ε” calculamos el límite cuando ε tiende a 0.
- En la segunda, toda una fila de la tabla es 0. Esta degeneración se salva montando al polinomio auxiliar de la fila inmediatamente superior a la que nos apareció la fila de ceros. A esta ecuación se le hace la derivada y lo que nos de se sustituye en la fila de ceros, pudiendo así continuar calculando. Al igual que en la anterior degeneración, para comprobar los cambios de signo se deja el 0 que nos apareció.
Si en el denominador de la función de transferencia del sistema tenemos una incógnita, se calcula de igual forma todo el criterio de Routh – Hürwitz y en las filas de la primera columna en la que nos aparezca la incógnita deberá ser su resultado mayor a 0, resolvemos las inecuaciones y cogemos los resultados más restrictivos, siendo estos los que nos determinen que el sistema sea estable.
Finalmente se puede comprobar haciendo Ruffini, y observaremos que en los que nos dio un 0 nos saldrá una par de polos complejos conjugados, si la parte real es negativa el par de polos complejos es estable, sino no se sabe si lo es.
Ejemplos
Ejemplo primera degeneración: G(s) = 

Esto nos da como resultado en la primera columna: 1, 1, 0, -α, 3, con lo que por haber dos cambios de signo, el sistema es inestable por poseer dos elementos en el semiplano derecho.
Ejemplo segunda degeneración: G(s) = 

Esto nos da como resultado en la primera columna: 1, 3, 2, 0, 2, con lo que la fila 4 es un línea de ceros la cual indica una oscilación permanete, es decir en el límite de la estabilidad.
SYS en el límite de la estabilidad
En el límite de la estabilidad, a través del teorema de Routh podemos saber si el sistema se encuentra en otro estado que no sea estable o inestable, y este es si se encuentras en el límite de la estabilidad, es decir se produce una oscilación mantenida, incluso en estado estacionario esta oscilación se mantendrá.
Esto se produce cuando en nuestra tabla de Routh alguna línea se puede hacer 0 y no haya ningún cambio de signo en nuestra primera columna. En este caso el sistema se encuentra en el límite de la estabilidad, esto representa en el plano complejo dos polos conjugados en el eje imaginarios (sin parte real). Un polo doble en el origen (doble integrador) no seria nuestro caso, ya que un polo en el origen genera inestabilidad. Podemos hallar el lugar de estos polos a través del polinomio auxiliar que obtenemos de la fila superior a la de ceros.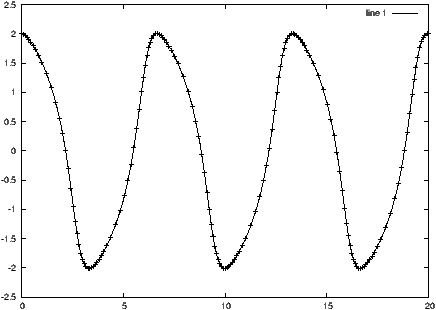

5.2 Lugar geométrico de las raíces
En teoría de control, el lugar de raíces o lugar de las raíces (del inglés, root locus) es el lugar geométrico de los polos y ceros de una función de transferencia a medida que se varía la ganancia del sistema K en un determinado intervalo.
El método del lugar de raíces permite determinar la posición de los polos de la función de transferencia a lazo cerrado para un determinado valor de ganancia K a partir de la función de transferencia a lazo abierto.
El lugar de raíces es una herramienta útil para analizar sistemas dinámicos lineales tipo SISO (single input single output) y su estabilidad (BIBO stability). (Recuérdese que un sistema es estable si todos sus polos se encuentran en el semiplano izquierdo del plano s (en el caso de sistemas continuos) o dentro del círculo unitario del plano z (para sistemas discretos).)
Definición
Sea  la función de transferencia del sistema a lazo abierto. Pertenecen al lugar de raíces todos los puntos del plano complejo que satisfacen la ecuación característica
la función de transferencia del sistema a lazo abierto. Pertenecen al lugar de raíces todos los puntos del plano complejo que satisfacen la ecuación característica
 la función de transferencia del sistema a lazo abierto. Pertenecen al lugar de raíces todos los puntos del plano complejo que satisfacen la ecuación característica
la función de transferencia del sistema a lazo abierto. Pertenecen al lugar de raíces todos los puntos del plano complejo que satisfacen la ecuación característica
Para el caso en que  , no se trata entonces del lugar de raíces verdadero, sino, del lugar de raíces complementario. Una solución de la ecuación para un valor de
, no se trata entonces del lugar de raíces verdadero, sino, del lugar de raíces complementario. Una solución de la ecuación para un valor de  dado se llama lugar de la raíz.
dado se llama lugar de la raíz.
 , no se trata entonces del lugar de raíces verdadero, sino, del lugar de raíces complementario. Una solución de la ecuación para un valor de
, no se trata entonces del lugar de raíces verdadero, sino, del lugar de raíces complementario. Una solución de la ecuación para un valor de  dado se llama lugar de la raíz.
dado se llama lugar de la raíz.Propiedades
Comienza en 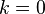 los polos
los polos  de la función de transferencia en lazo abierto
de la función de transferencia en lazo abierto  , y termina para
, y termina para  , normalmente con valor nulo. Las soluciones para
, normalmente con valor nulo. Las soluciones para 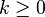 corresponden al lugar de raíces verdadero, mientras que las soluciones para
corresponden al lugar de raíces verdadero, mientras que las soluciones para 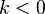 corresponden al lugar de raíces complementario.
corresponden al lugar de raíces complementario.
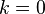 los polos
los polos  de la función de transferencia en lazo abierto
de la función de transferencia en lazo abierto  , y termina para
, y termina para  , normalmente con valor nulo. Las soluciones para
, normalmente con valor nulo. Las soluciones para 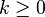 corresponden al lugar de raíces verdadero, mientras que las soluciones para
corresponden al lugar de raíces verdadero, mientras que las soluciones para 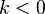 corresponden al lugar de raíces complementario.
corresponden al lugar de raíces complementario.Reglas para graficar el lugar de raíces
Las reglas que se detallan a continuación permiten graficar el lugar de raíces sin resolver la ecuación caracterísitica, permitiendo que el método sea aplicable a sistemas complejos. Se basan en el desarrollo de R. Evans, publicado en 1948, y por consiguiente se las conoce como Reglas de Evans.
Las siguientes reglas permiten graficar el lugar de raíces para valores de k positivos. Para valores negativos de k se utiliza un conjunto de reglas similar.
En lo que sigue, nos referimos a la función de transferencia a lazo abierto.
- Número de ramas. El número de ramas del lugar de raíces es igual al orden de la ecuación característica de la función de transferencia a lazo cerrado. Para sistemas racionales, esto equivale al orden de la ecuación característica de la función de transferencia a lazo abierto, es decir, el denominador de la función de transferencia a lazo abierto.
- Simetría. Dado que la ecuación característica es de coeficientes reales, las raíces complejas deben ser complejas conjugadas. Por tanto, el lugar de raíces es simétrico respecto al eje real.
- Polos de lazo abierto. Los polos de la función de transferencia a lazo abierto pertenecen al lugar de raíces y corresponden a
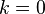 .
. - Ceros de lazo abierto. Los ceros de la función de transferencia a lazo abierto pertenecen al lugar de raíces y corresponden a
 . Si hay t polos más que ceros, entonces t posiciones se harán infinitas a medida que k se aproxime a infinito.
. Si hay t polos más que ceros, entonces t posiciones se harán infinitas a medida que k se aproxime a infinito. - Asíntotas. Si la función de transferencia de lazo cerrado tiene t polos más que ceros, entonces el lugar de raíces tiene tasíntotas equiespaciadas, formando entre ellas un ángulo de
 , donde
, donde  y
y  . El lugar de raíces se aproxima a estas asíntotas a medida que k tiende a infinito.
. El lugar de raíces se aproxima a estas asíntotas a medida que k tiende a infinito. - Centroide de las asíntotas. El punto del eje real donde las asíntotas se intersecan se suele llamar el centroide de las asíntotas, se denota mediante
 , y se calcula mediante
, y se calcula mediante  .
. - Lugar de raíces sobre el eje real. Si la función de transferencia a lazo abierto tiene más de un polo o cero reales, entonces el segmento del eje real que tiene un número impar de polos y ceros reales a su derecha forma parte del lugar de raíces.
- Puntos de entrada-salida. Los puntos de entrada-salida, o puntos singulares, indican la presencia de raíces múltiples de la ecuación característica, y se dan en los valores de s para los cuales se verifica
 .
. - Intersección con el eje imaginario. Las intersecciones con el eje imaginario se encuentran calculando los valores de k que surgen de resolver la ecuación característica para
 .
. - Pendiente del lugar de raíces en polos y ceros complejos (Condición de Argumento). La pendiente del lugar de raíces en polos y ceros complejos de la función de transferencia a lazo abierto se puede encontrar en un punto de la vecindad del polo o cero mediante la relación
 , para k>0, o
, para k>0, o  , para k<0.
, para k<0. - Cálculo de k en un punto del lugar de raíces (Condición de Modulo). El valor absoluto de k que corresponde a un punto dado del lugar de raíces puede determinarse midiendo el módulo de cada segmento que une cada polo y cero de la función de transferencia a lazo abierto y el punto en cuestión, y evaluando así
 .
.
5.2.1 Reglas generales para construir el
lugar geométrico de las raíces
5.2.2 Cancelación de los polos con G con
ceros H
Para un sistema complejo en lazo abierto con muchos polos y ceros, puede parecer com-plicado construir una gráfica del lugar geométrico de las raíces, aunque en realidad no es difícil si se aplican las reglas para construir dicho lugar geométrico. Ubicando los puntos y las asíntotas específicos y calculando los ángulos de salida de los polos complejos y los ángulos de llegada a los ceros complejos, podemos construir la forma general de los lugares geométricos de las raíces sin dificultad.
Reglas generales para construir los lugares geométricos de las raíces. Ahora resumiremos las reglas y el procedimiento general para construir los lugares geométricos de las raíces del sistema de la figura
Primero, obtenga la ecuación característica 1 + G(s)H(s) = 0
A continuación, vuelva a ordenar esta ecuación para que el parámetro de interés aparezca como el factor multiplicativo, en la forma
En estos análisis, suponemos que el parámetro de interés es la ganancia K, en donde K > 0.
(Si K < 0, lo cual corresponde al caso de realimentación positiva, debe modificarse la condición de angulo). Sin embargo, observe que el método todavía es aplicable a sistemas con parámetros de interés diferentes a la ganancia.
1. Ubique los polos y ceros de G(s)H(s) en el plano s. Las ramificaciones del lugar geométrico
de las raíces empiezan en los polos en lazo abierto y terminan en los ceros (ceros finitos o ceros
en infmito). A partir de la forma factorizada de la función de transferencia en lazo abierto, ubique
los polos y los ceros en lazo abierto en el plano s. [Observe que los ceros en lazo abierto son los de G(s)H(s), en tanto que los ceros en lazo cerrado son los de G(s) y los polos de H(s)].
2. Determine los lugares geométricos de las raíces sobre el eje real. Los lugares geométricos de las raíces sobre el eje real se determinan mediante los polos y los ceros en lazo abierto que se encuentran sobre él. Los polos y los ceros complejos conjugados de la función de transferencia en lazo abierto no afectan la ubicación de los lugares geométricos de las raíces sobre el eje real, porque la contribución del ángulo de un par de polos o ceros complejos conjugados es 360” sobre el eje real. Cada parte del lugar geométrico de las raíces sobre el eje real se extiende sobre un rango de un polo o cero a otro polo o cero. Al construir los lugares geométricos sobre el eje real, seleccione un punto en éste. Si la cantidad total de polos y ceros reales a la derecha de este punto de prueba es impar, este punto se encuentra en el lugar geométrico de las raíces El lugar geométrico de las raíces y su forma complementaria alternan segmentos a lo largo del eje real.
3. Determine las asíntotas de los lugares geométricos de las raíces. Si el punto de prueba s se ubica lejos del origen, se considera que no cambia el ángulo de cada cantidad compleja.
Entonces, un cero en lazo abierto y un polo en lazo abierto cancelan los efectos del otro. Por tanto, los lugares geométricos de las raíces para valores de muy grandes deben ser asintóticos para líneas rectas cuyos ángulos (pendientes) se obtengan mediante
Aquí,k = 0 corresponde a las asíntotas con el ángulo más pequeño con respecto al eje real.
Aunque k supone una cantidad infinita de valores, conforme aumenta, el ángulo se repite a sí mismo y la cantidad de asíntotas distintas es n-m.
Todas las asíntotas intersecan el eje real en un punto que se obtiene del modo siguiente: si se expanden el numerador y el denominador de la función de transferencia en lazo abierto, el resultado es
Si un punto de prueba se localiza muy lejos del origen, entonces, dividiendo el denominador entre el numerador, podemos escribir G(s)H(s) como
Dado que la ecuación característica es G(s)H(s) = - 1 puede escribirse como
4. Encuentre los puntos de desprendimiento y de ingreso. Debido a la simetría conju-gada de los lugares geométricos de las raíces, los puntos de desprendimiento y de ingreso se encuentran sobre el eje real o bien ocurren en pares complejos conjugados.
Si un lugar geométrico de las raíces se ubica entre dos polos en lazo abierto adyacentes sobre el eje real, existe al menos un punto de desprendimiento entre dichos dos polos.
Asimismo, si el lugar geométrico de las raíces está entre dos ceros adyacentes (un cero puede ubicarse en -∞) sobre el eje real, siempre existe al menos un punto de ingreso en-tre los dos ceros. Si el lugar geométrico de las raíces se ubica entre un polo en lazo abierto y un cero (finito o no finito) sobre el eje real, pueden no existir puntos de desprendimiento o de ingreso, o bien pueden existir ambos. Suponga que la ecuación característica se obtiene mediante
B(s) + KA(s) = 0
Los puntos de desprendimiento y los puntos de ingreso corresponden a las raíces múltiples de la ecuación característica. Por tanto, los puntos de desprendimiento y de ingreso se de-terminan a partir de las raíces de
en donde la prima indica una diferenciación con respecto a s. Es importante señalar que los puntos de desprendimiento y los puntos de ingreso deben ser las raíces de la ecuación anterior aunque no todas las raíces de la ecuación son puntos de desprendimiento o de ingreso real. Si una raiz real de la ecuación se encuentra en la parte del eje real del lugar geométrico de las raíces, es un punto de desprendimiento o de ingreso real. Si una raíz real de la ecuación no está en la parte del eje real del lugar geométrico, esta raiz no corresponde a u punto de desprendimiento ni a un punto de ingreso.
Si dos raíces s = s1 y s = -s1 de la ecuación son un par complejo conjugado, y si no es seguro que están en los lugares geométricos de las raíces, es necesario verificar el valor de K correspondiente. Si el valor de K que corresponde a la raíz s = s1 de dK/ds = 0 es positivo, el punto s = s1 es un punto de des-prendimiento o de ingreso real. (Dado que se supone que K es no negativo, si es negativo el valor obtenido de K, el punto s = s1 no es de desprendimiento ni de ingreso.)
5. Determine el ángulo de salida (ángulo de llegada) de un lugar geométrico de las raíces a partir de un polo complejo (un cero complejo). Para trazar los lugares geométricos de las raíces con una precisión razonable, debemos encontrar las direcciones de los lugares geométricos de las raíces cercanas a los polos y ceros complejos. Si se selecciona un punto de prueba y se mueve en la cercanía precisa del polo complejo (o del cero complejo), se considera que no cambia la suma de las contribuciones angulares de todos los otros polos y ceros. Por tanto, el ángulo de llegada (o ángulo de salida) del lugar geométrico de las raíces de un polo complejo (o de un cero complejo), se encuentra restando a 1800 la suma de to-dos los ángulos de vectores, desde todos los otros polos y ceros hasta el polo complejo (o cero complejo) en cuestión, incluyendo los signos apropiados.
Ángulo de salida desde un polo complejo = 180”
- (suma de los ángulos de vectores hacia el polo complejo en cuestión desde otros polos).
+ (suma de los ángulos de vectores hacia el polo complejo en cuestión desde los ceros).
Ángulo de llegada a un cero complejo = 180”
- (suma de los ángulos de vectores hacia el cero complejo en cuestión desde otro cero).
+ (suma de los ángulos de vectores hacia el cero complejo en cuestión desde los polos).
6. Encuentre los puntos en los que los lugares geométricos de las raíces cruzan el eje imaginario. Los puntos en donde los lugares geométricos de las raíces intersecan el eje jω se encuentran con facilidad por medio de: (a) el criterio de estabilidad de Routh, o (b) suponiendo que s = jo en la ecuación característica, igualando con cero la parte real y la parte imaginaria y despejando y K. En este caso, los valores encontrados de ω representan las frecuencias en las cuales los lugares geométricos de las raíces cruzan el eje imaginario. El valor de K que corresponde a cada frecuencia de cruce produce la ganancia en el punto de cruce.
7. Tomando una serie de puntos de prueba en la vecindad amplia del origen del plano s, trace los lugares geométricos. Determine los lugares geométricos de las raíces en la vecindad amplia del eje ω y el origen. La parte más importante de los lugares geométricos de las raíces no está sobre el eje real ni en las asíntotas, sino en la parte de la vecindad amplia del eje jo y el origen. La forma de los lugares geométricos de las raíces en esta región impor-tante del plano debe obtenerse con suficiente precisión.
8. Determine los polos en lazo cerrado. Un punto específico de cada ramificación del lugar geométrico de las raíces será un polo en lazo cerrado si el valor de K en dicho punto satisface la condición de magnitud. Por otra parte, la condición de magnitud nos permite determinar el valor de la ganancia en K en cualquier ubicación de las raíces específica sobre el lugar geométrico. (Si es necesario, se establece una graduación de los lugares geométricos en términos de K.Los lugares geométricos de las raíces son continuos con K.)
El valor de Kque corresponde a cualquier punto s sobre el lugar geométrico de las raíces se obtiene a partir de la condición de magnitud, o bien
Este valor puede calcularse en forma gráfica o analítica. Si en este problema se da la ganancia K de la función de transferencia en lazo abierto, entonces, aplicando la condición de magnitud encontramos las ubicaciones correctas de los polos en lazo cerrado para un K determinado de cada ramificación de los lugares geométricos de las raíces, mediante un enfoque de prueba y error o mediante MATLAB.
Comentarios acerca de las gráficas del lugar geométrico de las raíces. Se ob-serva que la ecuación característica del sistema cuya función de transferencia en lazo abierto es
es una ecuación algebraica en de n-ésimo grado. Si el orden del numerador de G(s)H(s) es menor que el del denominador, en dos o más (lo que significa que hay dos o más ceros en infinito), el coeficiente a1 es la suma negativa de las raíces de la ecuación y es independiente de K. En este caso, si alguna de las raíces se mueve en el lugar geométrico de las raíces hacia la izquierda, con-forme K aumenta, las otras raíces deben moverse hacia la derecha conforme aumenta K. Esta información es útil para encontrar la forma general de los lugares geométricos de las raíces.
También se observa que un cambio ligero en el patrón de los polos y ceros provoca cam-bios significativos en las gráficas del lugar geométrico de las raíces. La figura representa el hecho de que un cambio ligero en la ubicación de un cero o polo hará muy diferente la gráfica del lugar geométrico de las raíces.
Cancelación de los polos G(s) con los ceros de H(s). Es importante señalar que si el denominador de G(s) y el numerador de H(s) contienen factores comunes, los polos y ceros en lazo abierto correspondientes se cancelarán unos a otros, lo cual reducirá el grado de la ecuación característica en uno o más. Por ejemplo, considere el sistema de la figura (Este sistema tiene una realimentación de velocidad.) Si se modifica el diagrama de bloques de la figura para obtener el de la figura se aprecia con claridad que G(s) y H(s) tiene un factor común s + 1. La función de transferencia en lazo cerrado C(s)/R(s) es
La ecuación característica es
Sin embargo, debido a la cancelación de los términos + 1) que aparecen en G(s) y H(s), tenemos que
La ecuación característica reducida es
La gráfica del lugar geométrico de las raíces de G(s)H(s) no muestra todas las raíces de la ecuación característica; sólo las raíces de la ecuación reducida.
Para obtener el conjunto completo de polos en lazo cerrado, debemos agregar el polo cancelado de G(s)H(s) para los polos en lazo cerrado obtenidos en la gráfica del lugar geométrico de las raíces de G(s)H(s). No debe olvidarse que el polo cancelado de G(s)H(s) es un polo en lazo cerrado del sistema, como se observa en la figura.
Tabla Configuraciones de polos y ceros en lazo abierto y los correspondientes lugares geométricos de las raíces



















